Using shortcuts
You can enter and edit quite complex equations using just a few shortcuts

Alt+2,Cmd+2hide/show input cellCtrl+/make fraction on selectedCtrl+6make superscript on selectedCtrl+2make square root on selectedCtrl+-make subscript on selected
This is a syntax sugar borrowed from Mathematica, but implemented in a much simpler way
(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)
If you copy and paste into a normal text editor, what you see is a normal Woflram Language code
(*FractionBox[*)((1)(*,*)/(*,*)(2))(*]FractionBox*)
Wolfram Kernel can generate them as well like you can expect in Mathematica
Series[Sinc[(*SqB[*)Sqrt[x](*]SqB*)], {x,0,4}] // Normal
1-(*FB[*)((x)(*,*)/(*,*)(6))(*]FB*)+((*FB[*)((1)(*,*)/(*,*)(120))(*]FB*)) ((*SpB[*)Power[x(*|*),(*|*)2](*]SpB*))-(*FB[*)(((*SpB[*)Power[x(*|*),(*|*)3](*]SpB*))(*,*)/(*,*)(5040))(*]FB*)+(*FB[*)(((*SpB[*)Power[x(*|*),(*|*)4](*]SpB*))(*,*)/(*,*)(362880))(*]FB*)
Here is another example
n = (*SqB[*)Sqrt[1 - (*FB[*)(((*SpB[*)Power[(*SbB[*)Subscript[\[Omega](*|*),(*|*)p](*]SbB*)(*|*),(*|*)2](*]SpB*))(*,*)/(*,*)(((*SpB[*)Power[(*SbB[*)Subscript[\[Omega](*|*),(*|*)0](*]SbB*)(*|*),(*|*)2](*]SpB*) - 4Pi (*SpB[*)Power[\[Eta](*|*),(*|*)2](*]SpB*) ) - 2 Pi I \[Gamma] \[Eta]))(*]FB*) ](*]SqB*) ;
Then lets expand it into a series
Series[n, {\[Eta], 0, 1}]
(*VB[*)(SeriesData[\[Eta], 0, {Sqrt[(Subscript[\[Omega], 0]^2 - Subscript[\[Omega], p]^2)/Subscript[\[Omega], 0]^2], ((-I)*Pi*\[Gamma]*Subscript[\[Omega], p]^2*Sqrt[(Subscript[\[Omega], 0]^2 - Subscript[\[Omega], p]^2)/Subscript[\[Omega], 0]^2])/(Subscript[\[Omega], 0]^2*(Subscript[\[Omega], 0]^2 - Subscript[\[Omega], p]^2))}, 0, 2, 1])(*,*)(*"1:eJztVEtPwkAQRuPB+Csqp3atseUhwo0WyrtAtyBQegBboPLo9oFQ1N/l33O7NUZPKAnxYrKZnfl2Mq9vM5djW5mcxGIx7wyLsr0wJqehdYFF0bB82+1a5ga+4VcaQEfQAAMd19doIIU6TWMUhVrL3piuFppj4rQeew+uhXxtmOOSYpYGL4BhieR0GujYCzDMFzRBUITR69+HRHtCYpQFzA2RR6g4hHUJKwRxoh4+5jPMSZlUkSIxOXIJSeqAGva2SIL+E/RDgpiIisz3xEfIfAjXf0HA54iuaNAlPwearmV6hZE/0qJZsRTHUs+vLJUgh9ej4dEgzufM6lZVG3YLLuV5v5S3B9MiLD/N07X7RaMipHrzsiAHcFetb9y6KnItfioF8hiKYjqwfLVduPN81bqtZ+1E0ytUAmNXavB+yeHkci+PhFK7uPE7qNapNtrKfCAJSF3aWyFlKUv0aK3ShioqfbkGkSy0C73MjJvFw7r0Lu4n2mfhdlPWC9M7DxVzZDRXi4Cgqrs23wF1eFes"*)(*]VB*)
Using command palette
One can use a helper palette - Special characters panel for typing various mathematical operations

and then
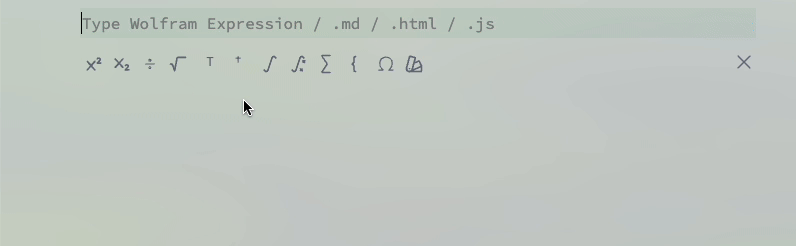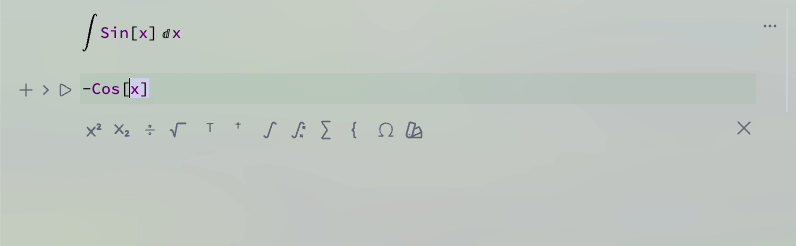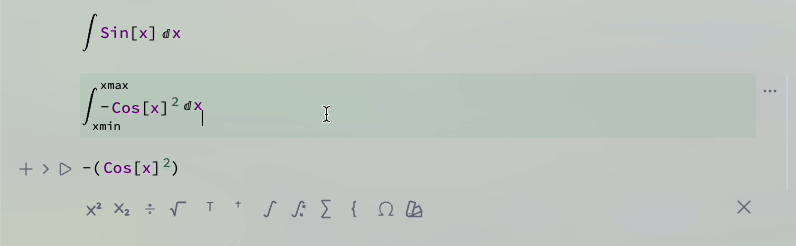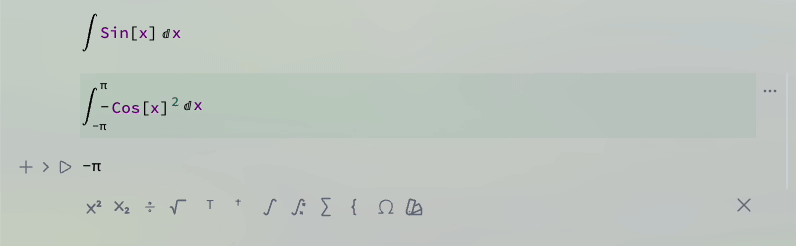
For example
(*TB[*)Integrate[(*|*)Sin[x](*|*), (*|*)x(*|*)](*|*)(*1:eJxTTMoPSmNiYGAo5gESnnklqelFiSWpTvkVmYwgUVYg4ZaYU5wKAMfBCcU=*)(*]TB*)
-Cos[x]
Or with defined boundaries
(*TB[*)Integrate[(*|*)Sin[x](*|*), {(*|*)x(*|*),(*|*)B(*|*),(*|*)A(*|*)}](*|*)(*1:eJxTTMoPSmNiYGAo5gESnnklqelFiSWpTvkVmYwgURYgEVJUmgoAvmMJeQ==*)(*]TB*)
-Cos[A]+Cos[B]
One can also use InputForm for taking integrals
Integrate[Sin[x], x]
-Cos[x]
Derivatives
It works in the same way
D[Sin[x]]
Cos[x]
Derivative of an undefined function holds it form
D[f[x], x]
(f')[x] /. {f -> Sin}
Cos[x]
Series
Symbolic series is also supported
(*TB[*)Sum[(*|*)(*SpB[*)Power[x(*|*),(*|*)2](*]SpB*)(*|*), {(*|*)x(*|*),(*|*)xmin(*|*),(*|*)xmax(*|*)}](*|*)(*1:eJxTTMoPSmNiYGAoZgMSwaW5TvkVmYwgPguQCCkqTQUAeAcHBQ==*)(*]TB*)
((*FB[*)((1)(*,*)/(*,*)(6))(*]FB*)) (1+xmax-xmin) (xmax+2 ((*SpB[*)Power[xmax(*|*),(*|*)2](*]SpB*))-xmin+2 xmax xmin+2 ((*SpB[*)Power[xmin(*|*),(*|*)2](*]SpB*)))
Input form is following
Sum[(*SpB[*)Power[x(*|*),(*|*)2](*]SpB*), {x, xmin, xmax}]
((*FB[*)((1)(*,*)/(*,*)(6))(*]FB*)) (1+xmax-xmin) (xmax+2 ((*SpB[*)Power[xmax(*|*),(*|*)2](*]SpB*))-xmin+2 xmax xmin+2 ((*SpB[*)Power[xmin(*|*),(*|*)2](*]SpB*)))
Piecewise
Piecewise given functions can also be constructed and differentiated
Plot[ (*TB[*)Piecewise[{{(*|*)Sin[x](*|*),(*|*)x > 0(*|*)},{(*|*)0(*|*),(*|*)True(*|*)}}](*|*)(*1:eJxTTMoPSmNkYGAo5gESAZmpyanlmcWpTvkVmUxAAQBzVQdd*)(*]TB*) , {x,-10,10}]
(*VB[*)(FrontEndRef["41a0ff8e-cf3a-4b6c-b31f-822a69cfc2ac"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKmxgmGqSlWaTqJqcZJ+qaJJkl6yYZG6bpWhgZJZpZJqclGyUmAwCS7RaI"*)(*]VB*)
Matrixes
There is a special snippet, which can help you to work with them. Type Insert Matrix in a command palette
((*GB[*){{1(*|*),(*|*)0(*|*),(*|*)0}(*||*),(*||*){0(*|*),(*|*)a(*|*),(*|*)0}(*||*),(*||*){0(*|*),(*|*)0(*|*),(*|*)1}}(*]GB*)).((*GB[*){{0(*|*),(*|*)0(*|*),(*|*)1}(*||*),(*||*){1(*|*),(*|*)0(*|*),(*|*)1}(*||*),(*||*){1(*|*),(*|*)0(*|*),(*|*)0}}(*]GB*)) // MatrixForm
((*GB[*){{0(*|*),(*|*)0(*|*),(*|*)1}(*||*),(*||*){a(*|*),(*|*)0(*|*),(*|*)a}(*||*),(*||*){1(*|*),(*|*)0(*|*),(*|*)0}}(*]GB*))
Greek letters
To enter Greek's symbols use ESC key and type the first letter. The autocomplete will suggest the corresponding letter. Or use Special Characters tool from the command palette
(*SpB[*)Power[{\[Alpha], \[Beta], \[Gamma]}(*|*),(*|*)2](*]SpB*)
{(*SpB[*)Power[\[Alpha](*|*),(*|*)2](*]SpB*),(*SpB[*)Power[\[Beta](*|*),(*|*)2](*]SpB*),(*SpB[*)Power[\[Gamma](*|*),(*|*)2](*]SpB*)}
Crazy and useless things
For colors and dates the decorations are also supported. For example
Table[RGBColor[i,j,1], {i,0,1,0.3}, {j,0,1,0.3}] // TableForm
(*GB[*){{(*VB[*)(RGBColor[0., 0., 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQAE644M9APZHE10="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0., 0.3, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQEGRMRhctoeKfLAHABMyFaE="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0., 0.6, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQEGRMRg8toeKfLAHABPiFbE="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0., 0.8999999999999999, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQEHRGTB4Yw8V+WAPAEhEGVA="*)(*]VB*)}(*||*),(*||*){(*VB[*)(RGBColor[0.3, 0., 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8Fl+yIGKIAyPtgDACeWFaE="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.3, 0.3, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8FlewSDAQw+2AMARHIX5Q=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.3, 0.6, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8FleyjjsX0RAxh8sAcARSIX9Q=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.3, 0.8999999999999999, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8Fl+6IzYPDGvogBDD7YAwB5hBuU"*)(*]VB*)}(*||*),(*||*){(*VB[*)(RGBColor[0.6, 0., 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8Fj+yIGKIAyPtgDACjWFbE="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.6, 0.3, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8Fjeyjjsn0RAxh8sAcARbIX9Q=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.6, 0.6, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8FjewSDAQw+2AMARmIYBQ=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.6, 0.8999999999999999, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcZg8Fj+6IzYPDGvogBDD7YAwB6xBuk"*)(*]VB*)}(*||*),(*||*){(*VB[*)(RGBColor[0.8999999999999999, 0., 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRedAYM39kUMUABlfLAHAH3PGVA="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.8999999999999999, 0.3, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRedAYM39kXGYHDZvogBDD7YAwCaqxuU"*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.8999999999999999, 0.6, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRedAYM39kXGYPDYvogBDD7YAwCbWxuk"*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0.8999999999999999, 0.8999999999999999, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRedAYM39ggGAxh8sAcAz70fQw=="*)(*]VB*)}}(*]GB*)