Notebook interface

An overview of an multipurpose editor

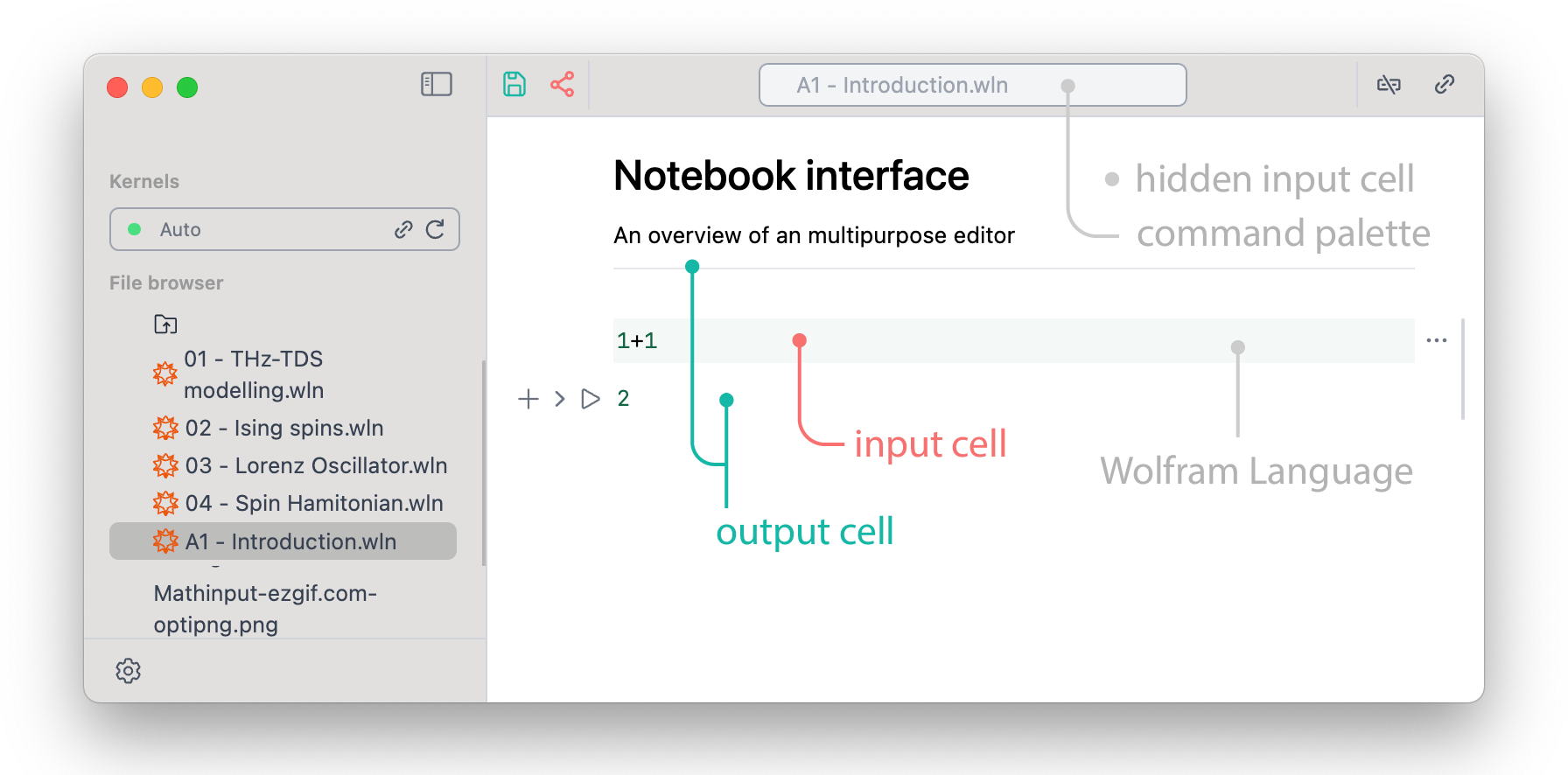
By the default any text in a new cell is considered to be Wolfram Language

1+1

To evaluate an expression press play icon or Shift+Enter

One can also hide any input cell by clicking on a ^ mark on the left side

Text cells

For typing regular text, embedding pictures, making description we use Markdown language.

To make markdown cell type in the first line of a new cell .md, if it was an anonymous file

.md

# Heading 1
## Heading 2

Here is a regular paragraph, which can __be styled__ in a *different way*. Then press `Shift+Enter` to make an output cell.

You can also hide an input cell automatically by a shortcut `Win/Cmd + 2`

$\\LaTeX$ is also supported

As well as regular HTML <span style="color:red">language</span>

Heading 1

Heading 2

Here is a regular paragraph, which can be styled in a different way. Then press Shift+Enter to make an output cell.

You can also hide an input cell automatically by a shortcut Win/Cmd + 2

$\LaTeX$ is also supported

As well as regular HTML

language

.md
To embed a picture type

![alt](https://upload.wikimedia.org/wikipedia/commons/a/a0/Kilroy_was_here_%28re-drawn%29.gif)

To embed a picture type

alt

Or just drag and drop any image file to a cell

One can also draw inside markdown cell using a special keyword

!! []

There are many more cell types are available. For example

Javascript

.js

return 1+1;


return 1+1;

Mermaid

.mermaid

graph LR
    A[Square Rect] -- Link text --> B((Circle))
    A --> C(Round Rect)
    B --> D{Rhombus}
    C --> D

graph LR
    A[Square Rect] -- Link text --> B((Circle))
    A --> C(Round Rect)
    B --> D{Rhombus}
    C --> D

Slides

.slide

# Here is a title

and many more!

Wolfram Language

A symbolic programming language

There are a few key-features compared to other languages

Data and code are indistinguishable.
It employs a pattern matching approach.
It features a versatile standard library, friendly for mathematicians and physicists.
It boasts a comprehensive standard library for visualizing data.
Provides powerful syntax sugar

Output cells are editable, you can evaluate it as well

{1,1,2,2,2,2} /. {2 -> 1, 1 -> 0}

{0,0,1,1,1,1}

rules are one of the most powerful features, i.e.

{0,0,1,1,1,1} /. {any_Integer :> any / 2}

{0,0,(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)}

And everything is a Symbol (or expression)

{0,0,(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)} /. {any_?NumericQ :> {RGBColor[any, 1-any, 1], any} }

{{(*VB[*)(RGBColor[0, 1, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQAGU8cEezgAAAxwUjA=="*)(*]VB*),0},{(*VB[*)(RGBColor[0, 1, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQAGU8cEezgAAAxwUjA=="*)(*]VB*),0},{(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)},{(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)},{(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)},{(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*),(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)}}

or may be you prefer tables

% // Transpose // TableForm

(*GB[*){{(*VB[*)(RGBColor[0, 1, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQAGU8cEezgAAAxwUjA=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[0, 1, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxQAGU8cEezgAAAxwUjA=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*)(*|*),(*|*)(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*)}(*||*),(*||*){0(*|*),(*|*)0(*|*),(*|*)(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)(*|*),(*|*)(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)(*|*),(*|*)(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)(*|*),(*|*)(*FB[*)((1)(*,*)/(*,*)(2))(*]FB*)}}(*]GB*)

Or something more complicated

Table[If[PrimeQ[i], Framed[i, Background->Yellow], i], {i, 1, 20}]

{1,(*BB[*)(2)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),(*BB[*)(3)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),4,(*BB[*)(5)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),6,(*BB[*)(7)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),8,9,10,(*BB[*)(11)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),12,(*BB[*)(13)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),14,15,16,(*BB[*)(17)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),18,(*BB[*)(19)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHArSsxNdcqvgIiA5INKc1KLuYAMp8Tk7PSi/NK8lDRmmPIgdyfn/Jz8okyQcRACiBnQdPMAGcElRZkF/nmeeQWlJcWsIJsSc4pTAcQ1Hcg="*)(*]BB*),20}

So-called 2D math input allows to enter complex equations, which looks similar to what you get used to see in textbooks.

\[Epsilon] = 1 + (*TB[*)Sum[(*|*)(*FB[*)(((*SbB[*)Subscript[f(*|*),(*|*)i](*]SbB*))(*,*)/(*,*)(((*SpB[*)Power[(*SbB[*)Subscript[\[Omega](*|*),(*|*)i](*]SbB*)(*|*),(*|*)2](*]SpB*) - (*SpB[*)Power[(*SbB[*)Subscript[\[Nu](*|*),(*|*)0](*]SbB*)(*|*),(*|*)2](*]SpB*))))(*]FB*)(*|*), {(*|*)i(*|*),(*|*)1(*|*),(*|*)3(*|*)}](*|*)(*1:eJxTTMoPSmNiYGAoZgMSwaW5TvkVmYwgPguQCCkqTQUAeAcHBQ==*)(*]TB*)

1+(*FB[*)(((*SbB[*)Subscript[f(*|*),(*|*)1](*]SbB*))(*,*)/(*,*)(-((*SpB[*)Power[((*SbB[*)Subscript[\[Nu](*|*),(*|*)0](*]SbB*))(*|*),(*|*)2](*]SpB*))+(*SpB[*)Power[((*SbB[*)Subscript[\[Omega](*|*),(*|*)1](*]SbB*))(*|*),(*|*)2](*]SpB*)))(*]FB*)+(*FB[*)(((*SbB[*)Subscript[f(*|*),(*|*)2](*]SbB*))(*,*)/(*,*)(-((*SpB[*)Power[((*SbB[*)Subscript[\[Nu](*|*),(*|*)0](*]SbB*))(*|*),(*|*)2](*]SpB*))+(*SpB[*)Power[((*SbB[*)Subscript[\[Omega](*|*),(*|*)2](*]SbB*))(*|*),(*|*)2](*]SpB*)))(*]FB*)+(*FB[*)(((*SbB[*)Subscript[f(*|*),(*|*)3](*]SbB*))(*,*)/(*,*)(-((*SpB[*)Power[((*SbB[*)Subscript[\[Nu](*|*),(*|*)0](*]SbB*))(*|*),(*|*)2](*]SpB*))+(*SpB[*)Power[((*SbB[*)Subscript[\[Omega](*|*),(*|*)3](*]SbB*))(*|*),(*|*)2](*]SpB*)))(*]FB*)

Any graphics object is also an expression!

Plot[x, {x,0,1}, PlotStyle -> (*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*)]

(*VB[*)(FrontEndRef["0abffd63-2484-4b4f-b2e2-f0e9e52c0377"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKGyQmpaWlmBnrGplYmOiaJJmk6SYZpRrpphmkWqaaGiUbGJubAwCNohXQ"*)(*]VB*) /. {(*VB[*)(RGBColor[1/2, 1/2, 1])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEDe3TGB3sAGJkVmw=="*)(*]VB*) -> Red}

(*VB[*)(FrontEndRef["e630c1ab-22ee-4894-bd4e-df01145b168a"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKp5oZGyQbJibpGhmlpuqaWFia6CalmKTqpqQZGBqamCYZmlkkAgCJYBXF"*)(*]VB*)

This is not a picture, this is a set of Wolfram Expressions covered with a decoration. Underneath there is still a working code

Or may be

Graphics3D[Sphere[]]

(*VB[*)(FrontEndRef["3a8e7b43-b8da-4fd7-8029-9fce36edb5d3"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKGydapJonmRjrJlmkJOqapKWY61oYGFnqWqYlpxqbpaYkmaYYAwCNjRZC"*)(*]VB*)/. {Sphere -> Cuboid}

(*VB[*)(FrontEndRef["167ffe0f-6f06-4ba9-ae2c-98abf947a7cc"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKG5qZp6WlGqTpmqUZmOmaJCVa6iamGiXrWlokJqVZmpgnmicnAwCPcxZx"*)(*]VB*)

Or play some sound

ListPlay[Table[Sin[2 π 50 t], {t, 0, 1, 1./2000}]]

(*VB[*)(FrontEndRef["f51f5383-6cd0-41da-a191-c1bc8c4a6f6b"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKp5kappkaWxjrmiWnGOiaGKYk6iYaWhrqJhsmJVskmySapZklAQCEkRX4"*)(*]VB*)

Notebook interface

Text cells​

Heading 1

Heading 2​

Javascript​

Mermaid​