Musical scales and chords maker

· 9 min read

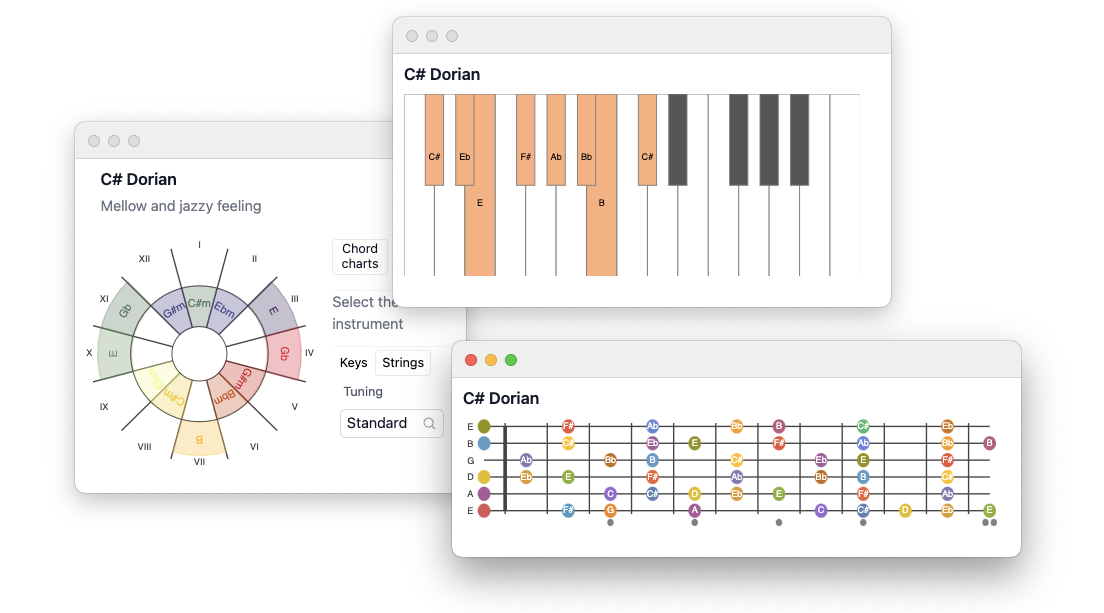
A multi-window app for deriving chords based on provided key and musical scale. The whole purpose is to quickly show on piano or guitar fingerboard all positions for the given combination of two. Charts are interactive - click to hear the sound

Features

Support for custom strings tuning
Circle of Fifth generation
Piano & Guitar fingerboard view
Sound preview
Pentatonics & normal scales

Download App v.01

How it works

Music theory

This app itself consists of small framework to work with SoundNote, which helps to make chords and mess with notes combinations. Here is a part of it

convertToSemitones[s_String] := With[{c = StringCases[s, {a__~~b:DigitCharacter :> {a,ToExpression[b]}, a__ :> {a,4}}]//First},
  semitone[c[[1]]] + (c[[2]] - 4) 12
]
convertToSemitones[s_] := s;

convertToSemitones[l_List] := convertToSemitones /@ l

semitone[0] = "C";
semitone[1] = "C#";
semitone[2] = "D";
semitone[3] = "D#";
semitone[3] = "Eb";
semitone[4] = "E";
semitone[5] = "F";
semitone[6] = "F#";
semitone[6] = "Gb";
semitone[7] = "G";
semitone[8] = "Ab";
semitone[8] = "G#";
semitone[9] = "A";
semitone[10] = "Bb";
semitone[11] = "B";

semitone[n_Integer] :=  semitone[Mod[n, 12]] /; n>11 

semitone["C"] = 0;
semitone["C#"] = 1;
semitone["D"] = 2;
semitone["D#"] = 3;
semitone["Eb"] = 3;
semitone["E"] = 4;
semitone["F"] = 5;
semitone["F#"] = 6;
semitone["Gb"] = 6;
semitone["G"] = 7;
semitone["Ab"] = 8;
semitone["G#"] = 8;
semitone["A"] = 9;
semitone["Bb"] = 10;
semitone["B"] = 11;

scale["Major"] = {2,2,1,2,2,2,1};
mood["Major"] = "Bright and upbeat feeling";
scale["Major Pentatonic"] = {2, 2, 3, 2, 3};
mood["Major Pentatonic"] = "Joyful and open feeling";
scale["Minor"] = {2,1,2,2,1,2,2};
mood["Minor"] = "Sad and reflective feeling";
scale["Minor Pentatonic"] = {3, 2, 2, 3, 2};
mood["Minor Pentatonic"] = "Bluesy and soulful feeling";
scale["Dorian"] = {2,1,2,2,2,1,2};
mood["Dorian"] = "Mellow and jazzy feeling";
scale["Lydian"] = {2,2,2,1,2,2,1};
mood["Lydian"] = "Dreamy and mystical feeling";
scale["Mixolydian"] = {2,2,1,2,2,1,2};
mood["Mixolydian"] = "Bluesy and relaxed feeling";
scale["Phrygian"] = {1,2,2,2,1,2,2};
mood["Phrygian"] = "Exotic and tense feeling";

majorQ[SoundNote[n_List]] := With[{notes = Sort[convertToSemitones @ n]},
  notes[[2]] - notes[[1]] > 3
]

makeScale[root_Integer, scale_List] := With[{base = Accumulate[Join[{root}, scale]]},
  (base[[Mod[#-1, Length[base]-1] + 1]] + 12 Floor[# / Length[base]]) &
]

makeScale[root_String, scale_List] := makeScale[convertToSemitones[root], scale]

makeChord[root_, scalename_String, ext_Integer:3] := With[{s = makeScale[root, scale[scalename]]},
  chordObject[s, ext]
]

NoteTranspose[SoundNote[l_List], i_Integer] := With[{c = convertToSemitones[l]}, 
  SoundNote[Map[(# + i)&, c]]
]

NoteTranspose[SoundNote[l_Integer], i_Integer] := With[{c = convertToSemitones[l]}, 
  SoundNote[c + i]
]

NoteMerge[s:(SoundNote[_List]..)] := SoundNote[DeleteDuplicates[convertToSemitones[Join @@ ({s}[[All,1]])]]]


makeChord[root_, scalename_String, ext_String];
makeChord[root_, scalename_String, ext_Integer, mod_Rule];
makeChord[root_, scalename_String, ext_Integer, mod:{__Rule}];

chordObject[s_, ext_][offset_String] := chordObject[s, ext][FromRomanNumeral[offset]-1]

chordObject[s_, ext_][offset_Integer] := SoundNote @ Table[  s[i + offset], {i, 1, 2 ext, 2}] 

NoteNormalize[SoundNote[l_List], {min_, max_}] := With[{notes = convertToSemitones @ l},
  SoundNote[With[{mod = Mod[#, max]}, If[mod < min, mod + min, mod]] &/@ notes // DeleteDuplicates]
]

Using that one can create tonic chord in given scale by simply calling

makeChord["C", "Major", 3][0]

and extend it

makeChord["C", "Major", 5][0]

Search bar

It is 100% based on the default input element InputAutocomplete with a search function made using StringMatchQ. Firstly the string is broken into words and then we count number of matches with the following pattern

StringMatchQ[scaleWord, ___~~inputWord~~___]

Circle of Fifth

We built chords from scales and then categorize each using a function majorQ. Circle consists of multiple lines and filled clickable pads with polygons made in a funny way

pad2 = With[{
c2 = {Cos[ Pi/2 - Pi/12], Sin[ Pi/2 - Pi/12]} // N,
c3 = {Cos[1 2Pi/12 + Pi/2 - Pi/12], Sin[1 2Pi/12 + Pi/2 - Pi/12]} //N 
},
  RegionIntersection[RegionDifference[Polygon[{c2 0.1, 1.5 c2, 1.5 c3, c3 0.1}], Disk[{0,0}, 0.25]],
    Disk[{0,0}, (0.75+0.5)/2]
  ]
] // BoundaryDiscretizeRegion // MeshCoordinates // Polygon;

pad1 = With[{
c2 = {Cos[ Pi/2 - Pi/12], Sin[ Pi/2 - Pi/12]} // N,
c3 = {Cos[1 2Pi/12 + Pi/2 - Pi/12], Sin[1 2Pi/12 + Pi/2 - Pi/12]} //N 
},
  RegionIntersection[RegionDifference[Polygon[{c2 0.1, 1.5 c2, 1.5 c3, c3 0.1}], Disk[{0,0}, (0.75+0.5)/2]],
    Disk[{0,0}, (((0.75 + 1)/2.0) + 1)/2.0]
  ]
] // BoundaryDiscretizeRegion // MeshCoordinates // Polygon;

then it is assembled into a circle

circleFifth[key_, scale_] := Graphics[{Table[With[{
  c1 = {Cos[-i 2Pi/12 + Pi/2], Sin[-i 2Pi/12 + Pi/2]},
  c2 = {Cos[-i 2Pi/12 + Pi/2 - Pi/12], Sin[-i 2Pi/12 + Pi/2 - Pi/12]} //N,
  chord = makeChord[key, scale, 3][i]
}, {

  Line[{0.25 c2, c2}],
  Text[RomanNumeral[i+1], c1, {0,0}],
  
  {Opacity[0.3], ColorData[35][i+6], Rotate[If[majorQ[chord], {
    EventHandler[pad1, {"click" -> Function[Null, NoteNormalize[NoteMerge[chord, NoteTranspose[chord, 12]], {12,24+12}] // Sound // EmitSound]}],
    Opacity[1], Directive[FontSize->12], Text[semitone[chord[[1,1]]], pad1 // RegionCentroid, {0,0}]
  }, {
    EventHandler[pad2, {"click" -> Function[Null, NoteNormalize[NoteMerge[chord, NoteTranspose[chord, 12]], {12, 24+12}] // Sound // EmitSound]}],
    Opacity[1], Directive[FontSize->12], Text[semitone[chord[[1,1]]] <> "m", pad2 // RegionCentroid, {0,0}]
  }], i 2 Pi/12, {0,0}]}
}], {i, 0,11}],

Circle[{0,0}, 0.25],
Circle[{0,0}, (0.75+0.5)/2]

}, "Controls"->False, ImageSize->{250,250}]

Here we assigned to each pad a handler, which emits sound on click. For example

circleFifth["F", "Major"]

Piano view

This is bunch of white and black rectangles

keyLevels = {0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0};
generateKeys[keyCount_] := Module[
  {index = 1, position = 1, keyWidth, keyOffset},
  Table[
    With[
      {
        cycleIndex = Mod[index - 1, 12] + 1,
        level = keyLevels[[Mod[index - 1, 12] + 1]]
      },
      keyWidth = 0.5 - 0.2 level;
      keyOffset = 0.5 level;
      position += 1 - level;
      index++;
      Rectangle[
        {position - keyWidth + keyOffset, keyOffset},
        {position + keyWidth + keyOffset, 1}
      ]
    ],
    {keyCount}
  ]
];

annotateKeys[keys_] := MapIndexed[
  Annotation[#, keyLevels[[Mod[#2[[1]] - 1, 12] + 1]], #2[[1]]] &,
  keys
];

highlightNotes[skeys_, indexes_] := Map[Function[key,
  If[MemberQ[indexes, key[[3]]], 
    {(*VB[*)(RGBColor[1., 0.6862745098039216, 0.47843137254901963])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeGJAIcndyzs/JLwouTyxJzghJzS3ISSxJTWMGyXMgyRcxgMEH+6JvX0HgqX3R/HkgcM8eAIGmHxI="*)(*]VB*), key}
  ,
    key
  ]
], skeys]

separateKeys[keys_] := Module[
  {annotatedKeys = annotateKeys[keys]},
  {
    Cases[annotatedKeys, Annotation[_, 0, _]],
    Cases[annotatedKeys, Annotation[_, 1, _]]
  }
];


clicker[scene_, separated_, keys_, additional_:{}, notes_, scale_:False][xy_] := With[{
  whiteMatch = SelectFirst[separated[[1]], RegionMember[#[[1]], xy]  &],
  blackMatch = SelectFirst[separated[[2]], RegionMember[#[[1]], xy]  &]
},

  With[{
    key = If[!MissingQ[blackMatch], blackMatch[[3]], whiteMatch[[3]]]
  },
  
    If[scale === False, With[{group = FrontInstanceGroup[]}, 
      
      FrontSubmit[NoteTranspose[SoundNote[Join[additional, {key-1}]//DeleteDuplicates], 12] // Sound];
      FrontSubmit[{
        Red, Text[notes[[Mod[# - 1, 12] + 1]], 
        Mean[List @@ (keys[[#]])] - {0,0.2}, {0,0}] &/@ Join[(Mod[#, Length[keys]-1] &/@ additional)+1, {key}], 
        Opacity[0.3], keys[[Join[((Mod[#, Length[keys]-1]) &/@ additional)+1, {key}]]]
      } // group, scene];
    
      SetTimeout[Delete[group], 200];
      Return[]
    ]];

    With[{sorted = Join[additional, {key-1}]//DeleteDuplicates // Sort},
      Do[With[{note = sorted[[i]], window = CurrentWindow[]},
        SetTimeout[
          FrontSubmit[NoteTranspose[SoundNote[note], 12] // Sound, "Window"->window];
          With[{group = FrontInstanceGroup[]},
            FrontSubmit[{
                    Red, Text[notes[[Mod[# - 1, 12] + 1]], 
                    Mean[List @@ (keys[[#]])] - {0,0.2}, {0,0}] &/@ Join[(Mod[#, Length[keys]-1] &/@ {note})+1, {key}], 
                    Opacity[0.3], keys[[Join[((Mod[#, Length[keys]-1]) &/@ {note})+1, {key}]]]
            } // group, scene, "Window"->window];   
            SetTimeout[Delete[group], 400];
          ];
        , (i-1)400 + 10];
      ], {i, Length[sorted]}]
    ];

    
  ]
]


ClearAll[PianoView];
PianoView[] := PianoView[SoundNote[{}]]
PianoView[SoundNote[rawNotes_List], OptionsPattern[]] := Module[{
  keys, separated, scene, scaleMode = False,
  highlighted, names = {"C", "C#", "D", "Eb", "E", "F", "F#", "G", "Ab", "A", "Bb", "B", "C"}, annotations,
  notes = convertToSemitones @ rawNotes
},
  keys = generateKeys[OptionValue["Size"]];

  separated = separateKeys[keys];

  scene = FrontInstanceReference[];

  highlighted = Mod[#, Length[keys]] + 1 &/@ notes;
  annotations = Text[names[[Mod[#, 12]+1]], Mean @ (
    List @@ keys[[Mod[#, Length[keys]] + 1]]
  ) + {0.,-0.1}, {0,0}] &/@ notes;

  notes = Switch[OptionValue["Mode"],
    "Play",
      notes,

    "Show",
      {},

    "Scale",
      scaleMode = True; notes,
    _,
      notes
  ];

  Graphics[{scene,
    {White, EdgeForm[Gray], highlightNotes[separated[[1]], highlighted], Black//Lighter, highlightNotes[separated[[2]],highlighted]},
    {Yellow, Opacity[0.3]}, {Black, annotations},
  EventHandler[Graphics`Canvas[], {"click" -> clicker[scene, separated, keys, notes, names, scaleMode]}]
  }, ImageSize->OptionValue[ImageSize], "Controls"->False]
]

Options[PianoView] = {ImageSize->{500,200}, "Size"->25, "Mode"->"Play"};

Heres as one can see, we don't assign event handlers to individual key, but report the exact coordinates of a click to clicker. Then it finds intersections with rectangles and emits sound.

For example

PianoView[SoundNote[{"G5", "A5", "B" }], "Mode"->"Scale"]

Guitar view

This is a bit tricky, since we have to support custom tunings as well as highlighting all possible ways of making the same note using different positions on the fingerboard

plucker[scene_, board_, highlighted_, additional_, scaleQ_][xy_] := With[{
  match = SelectFirst[board//Values//Flatten, With[{reg = Disk[#[[1,1]], #[[1,2]] * 2] },
    RegionMember[reg, xy]
  ]&]
},
  If[MissingQ[match], Return[]];
  With[{
    notes = Sort[Join[additional, {match[[2]]}]//DeleteDuplicates],
    client = CurrentWindow[]
  },

    If[scaleQ,
      MapIndexed[Function[{val, index},
        SetTimeout[With[{group = FrontInstanceGroup[]},
        
          FrontSubmit[SoundNote[val, "8n"] // Sound, "Window"->client];
          FrontSubmit[{
            Opacity[0.7], highlighted[{val}, Red]
          } // group, scene, "Window"->client];
  
          SetTimeout[Delete[group], 450]; 
          
        ], 450 * (index[[1]]-1) + 1]
      ], notes];   
    ,
      With[{group = FrontInstanceGroup[]},
        FrontSubmit[SoundNote[notes] // Sound];
        FrontSubmit[{
          Opacity[0.7], highlighted[notes]
        } // group, scene];
  
        SetTimeout[Delete[group], 200];   
      ]
    ]
  ]  
]


GuitarView[SoundNote[rawNotes_List], OptionsPattern[]] := Module[{
  tuning = convertToSemitones @ OptionValue["Tuning"],
  scene = FrontInstanceReference[],
  scaleQ = False,
 names = {"C", "C#", "D", "Eb", "E", "F", "F#", "G", "Ab", "A", "Bb", "B", "C"}, annotations,
  notes = convertToSemitones @ rawNotes,
  board, highlighted,
  semitoneTuning = Reverse[convertToSemitones @ OptionValue["Tuning"]]
},

notes = Switch[OptionValue["Mode"],
    "Play",
      notes,

    "Show",
      {},

    "Scale",
      scaleQ = True;
      notes,

    _,
      notes
  ];

notes = With[{c = Mod[#, convertToSemitones @ (semitoneTuning[[-1]] + 12)]},
  If[c < semitoneTuning[[1]],
    c + 12
  ,
    c
  ]
] &/@ notes;

board = GroupBy[Flatten[
  Table[With[{note = semitoneTuning[[y]] + x},
    Annotation[Disk[{x,y}, {0.15, 0.15 2.8 }], note, names[[Mod[note, 12]+1]]]
  ], {x, 0, 12}, {y, Length[tuning]}]
], #[[2]] &];

highlighted[notes_, color_:Automatic] := {
  If[color === Automatic, ColorData[97], color&] /@ Range[notes // Length],
  Map[Function[place, 
    If[place[[1,1,1]] > 0.5,
      {place, White, Text[place[[3]] , place[[1,1]]- {0,0.16}, {0,-1}]}
    ,
      place
    ]
  ], board[#]] &/@ notes
}//Transpose;

Graphics[{
  scene, EventHandler[Graphics`Canvas[], {"click"->plucker[scene, board, highlighted, notes, scaleQ]}],
  Table[Line[{{0, string}, {12, string}}], {string, Length[tuning]}],
  Table[Line[{{i - 0.5, 1 - 0.2 }, {i - 0.5, Length[tuning] + 0.2}}], {i, 12}],
  Table[Text[semitone[tuning[[Length[tuning] + 1 - string]]], {-0.4, string - 0.2}, {-1,-1}], {string, Length[tuning]}],
  {
    AbsoluteThickness[4], Line[{{0.5, 1}, {0.5, Length[tuning]}}], 
    Gray, Table[Disk[{0.5 + 2.5 + k, 0.3}, {0.15, 0.15 2.8 }/2], {k, 0, 6, 2}],
    Disk[{0.5 + 2.5 + 8.9, 0.3}, {0.15, 0.15 2.8 }/2], Disk[{0.5 + 2.5 + 9.1, 0.3}, {0.15, 0.15 2.8 }/2]
  },
  
  highlighted[notes]
  
}, ImageSize->OptionValue[ImageSize], "Controls"->False, ImagePadding->None, PlotRange->{{0 - 0.5, 12 + 0.5}, {0, Length[tuning] + .5}}]
]

Options[GuitarView] = {"Tuning"->({"E4", "A4", "D5", "G5", "B5", "E6"}//Reverse), "Mode"->"Play", ImageSize->(1.2 {500,100})}

The idea with emitting sound is the same as for piano. For example

GuitarView[SoundNote[{"E4", "G5", "B4"}], "Mode"->"Scale"]

It is done in the most basic way - by calling CellPrint with target _. To give more freedom to the customization of UI look we mostly use WLX to make a layout we pass the generated template directly to CellPrint and call it an option "Display"->"wlx". In this way it bypasses all cell-specific decorations and renders a raw HTML in the window (no blinking cursor or other attributes of the notebook cells).

How it works​

Music theory​

Search bar​

Circle of Fifth​

Piano view​

Guitar view​

Navigation between windows​