Skip to main content

Simples example of the Planar Inverse Kinematics

· One min read
Kirill Vasin

src. [FOUNDRY](https://learn.foundry.com/modo/content/help/pages/animation/modifiers/planar_ik.html)
Download original notebook

the actual implemntation is not well-optimized for Wolfram Language, but serves a good purpose for the demonstration

Define a bunch of points connect them into a segmented line with fixed length

chain = Table[Exp[-ϕ]{-Cos[ϕ], Sin[ϕ]}, {ϕ, 0, π - π/7, π/7.0}];
Graphics[{
    Line[chain // Offload], Black, 
    PointSize[0.04], Point[chain // Offload], Red,
    EventHandler[Graphics`Canvas[], {
      "mousemove" -> handler
    }]
  },
  Axes->True, PlotRange->{{-1,0.2}, {0,0.4}}, ImageSize->400
]

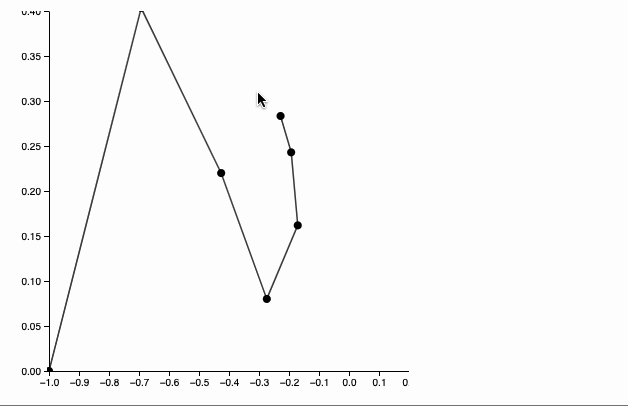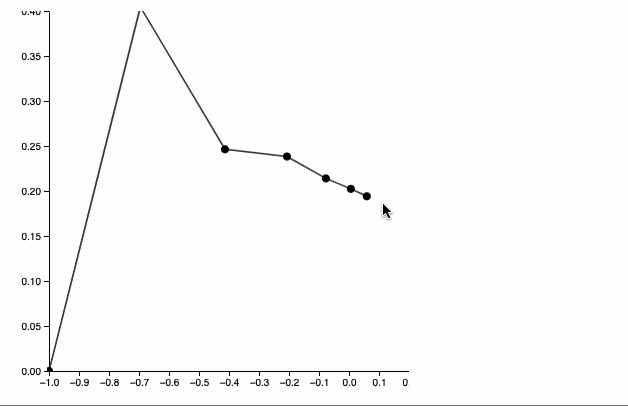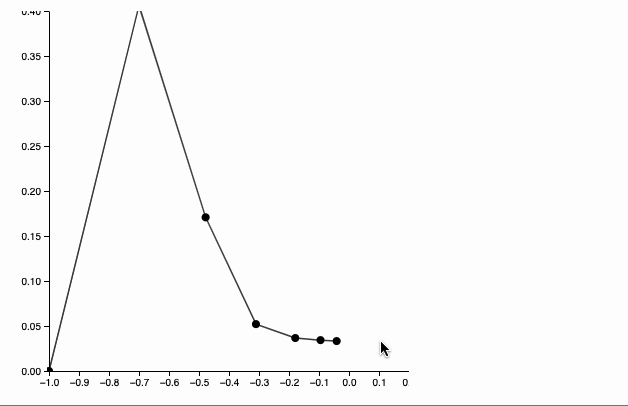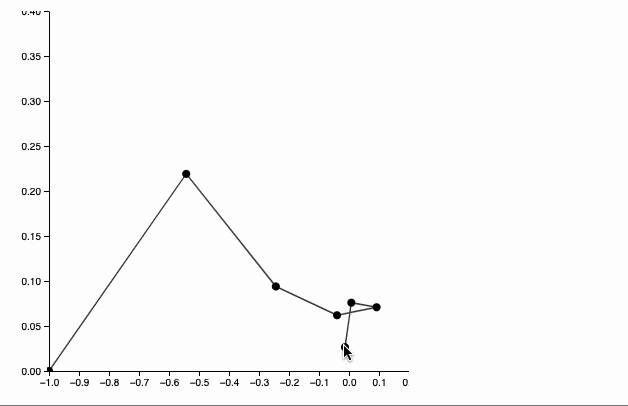
Dynamics is not available on this page. Download this notebook and run it

FABRIK Solver​

Original paper published in 2011

For the demonstration purposes, we implemented this in the simples possible way.

handler = Function[target,
  Module[{buffer = chain, origin = {-1,0}, prev = chain, lengths = Norm /@ (chain // Reverse // Differences) // Reverse},
    buffer = Table[With[{p = chain[[-i]]},
      If[i === 1,
        prev = target;
        target
      ,
    
        prev = prev - Normalize[(prev - p)] lengths[[1-i]];
        prev 
      ]
    ]   
    , {i, chain // Length}] // Reverse;

    buffer = Table[With[{p = buffer[[i]]},
      If[i === 1,
        prev = origin;
        origin
      ,
    
        prev = prev - Normalize[(prev - p)] lengths[[i-1]];
        prev 
      ]
    ]
    , {i, chain // Length}];

    chain = buffer;
   ]
];