Skip to main content

Line

WLJS
Execution environment
Supports dynamics
wljs-graphics-d3
Package

the representation of a line going though the points {x1,y1}, {x2,y2}

Line[{{x1,y1}, {x2,y2}, ...}]

or with multiple datasets

Line[{list1, list2, ...}]

General properties​

Line itself does not depend on its interpretation, you can also think about it if it was an abstract object like

ArcLength[Line[{{0, 0}, {1, 1}}]]

gives

Sqrt[2]

without Graphics used here.

Parameters​

There are certain parameters, that can affect the style of a line

AbsoluteThickness​

The default is 1

{AbsoluteThickness[3], Line[{{0,0}, {1,1}}]} // Graphics

Absolute thickness is indifferent to scaling or zooming of a graphics object.

RGBColor​

Specifies the color of a stroke

{Red, Line[{{0,0}, {1,1}}]} // Graphics

Indexed geometry​

Using it inside GraphicsComplex allows to specify only the indexes of vertices as arguments similar to faces like in Indexed geometry

Examples​

Simple primitive​

A line, that goes though list of points in 2D

Graphics[Line[{{1, 0}, {2, 4}, {3, 0}, {4, 4}}]]

or styled line

Graphics[{
  AbsoluteThickness[3],
  Red, 
  Line[{{1, 0}, {2, 1}, {3, 0}, {4, 1}}]
}]

Tangent vectors along an elliptic curve

With[{f = {Cos[x] + Sin[x], Sin[x]}}, 
 Graphics[
  Table[{LABColor[t/(2 Pi), 1, .8], Line[{f, Normalize[D[f, x]] + f}]} /. x -> t, {t, 0, 2 Pi, .1}]]]

Dynamics​

This is a main ingredient for displaying any dynamic plots, since Plot function works only for the static data.

Manipulation​

For example a live plot of traveling wave-packet

cell 1
packet[x_, t_] := Sum[Sin[- w t + w x], {w, 0,3,0.05}] / 10;
line = Table[{x, packet[x, 0]}, {x, 0, 10, 0.1}];
Graphics[Line[line // Offload], Frame->True, FrameLabel->{{"amplitude"}, {"distance"}}]

and a InputRange to control a time variable

cell 2
EventHandler[InputRange[0,5,0.5, 0], Function[t, 
  line = Table[{x, packet[x, t]}, {x, 0, 10, 0.1}];
]]

The desired result should look like

Inverse kinematics (FABRIK)​

This is an example of implementation FABRIK algorithm

Define a bunch of points connect them into a segmented line with fixed length

chain = {Cos[#[[1]]], Sin[#[[2]]]}&/@ RandomReal[{-1,1}, {65, 2}] // Sort;
lengths = Norm /@ (chain // Reverse // Differences) // Reverse;

the actual implementation of FABRIK

fabrik[lengths_, target_, origin_] := Module[{buffer, prev},
  buffer = Table[With[{p = chain[[-i]]},
    If[i === 1,
      prev = target;
      target
    ,
    
      prev = prev - Normalize[(prev - p)] lengths[[1-i]];
      prev 
    ]
  ], {i, chain // Length}] // Reverse;

  Table[With[{p = buffer[[i]]},
    If[i === 1,
      prev = origin;
      origin
    ,
    
      prev = prev - Normalize[(prev - p)] lengths[[i-1]];
      prev 
    ]
  ], {i, chain // Length}]
]

Dynamic visualization using lines and points

Graphics[{

  Line[chain // Offload], 
  Red, PointSize[0.06], 
  EventHandler[Point[{-1,-1}], {"drag"->Function[xy, chain = fabrik[lengths, xy, chain // First]]}], 
  Blue, Point[origin // Offload]
  
}, PlotRange->{{-2,2}, {-2,2}}, ImageSize->500, TransitionType->"Linear", TransitionDuration->30]

Try to drag a red dot using mouse The result will look like

note

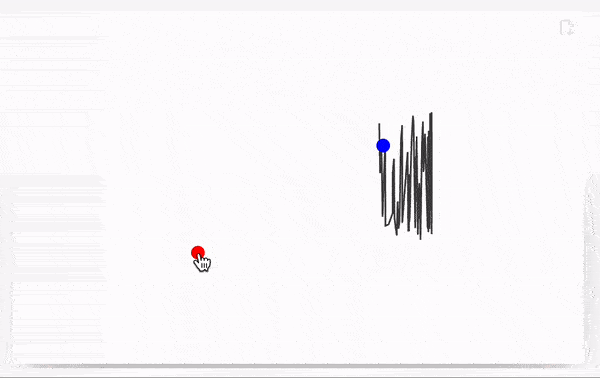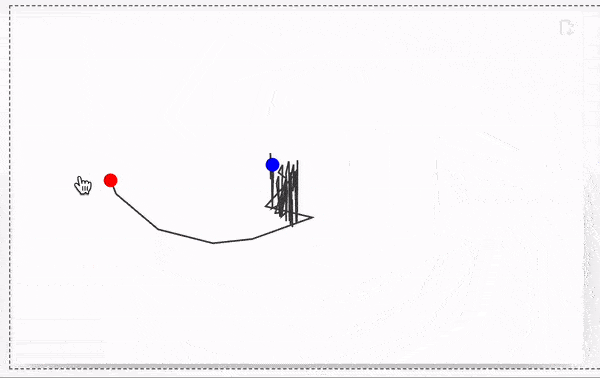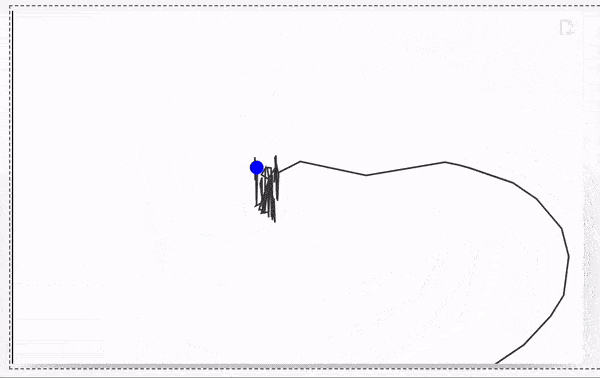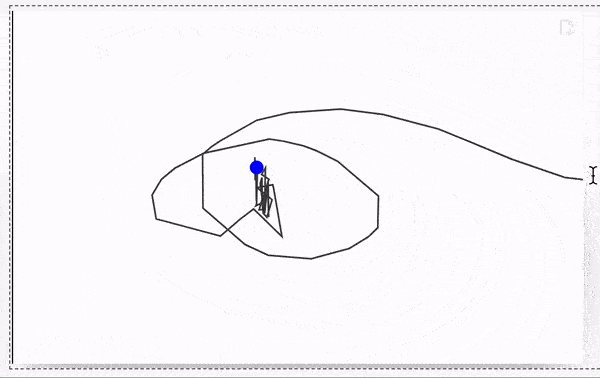
Line interpolates missing segments of a line, if the dataset has been updated. No actions needed form the user

Last updated on