GeometricTransformation
GeometricTransformation[object_, matrix3x3_List]
applies general matrix3x3 to each vertex of an object, i.e. replacing each point p by matrix3x3.p
GeometricTransformation[object_, vector3_List]
applies translation vector3 to each vertex of an object
GeometricTransformation[object_, {matrix3_List, vector3_List}]
applies transformation matrix and translation operation matrix3.p + vector3
info
object can be nested or group of graphics primitives as well
Examples
Graphics3D[
GeometricTransformation[Sphere[], N@ShearingMatrix[2, {1,1,1}, {1,1,0}]]
]
tip
Numerical matrixes are usually faster. Use N to get pure numbers
Or more complicated one
Graphics3D[
GeometricTransformation[Cuboid[{0, 0, 0}, {1.5, 1.5, .2}],
Table[{RotationMatrix[a, {0, 0, 1}], {Cos[a], Sin[a], a}}, {a, 0,
4 Pi, .2}]], Boxed -> False]
Dynamics
It fully supports updates. See example
cell 1
rot = RotationMatrix[45 Degree, {0, 0, 1}];
stair = GeometricTransformation[Cuboid[{0, 0, 0}, {1.5, 1.5, .2}],
Table[{RotationMatrix[a, {0, 0, 1}], {Cos[a], Sin[a], a}}, {a, 0,
4 Pi, .2}]];
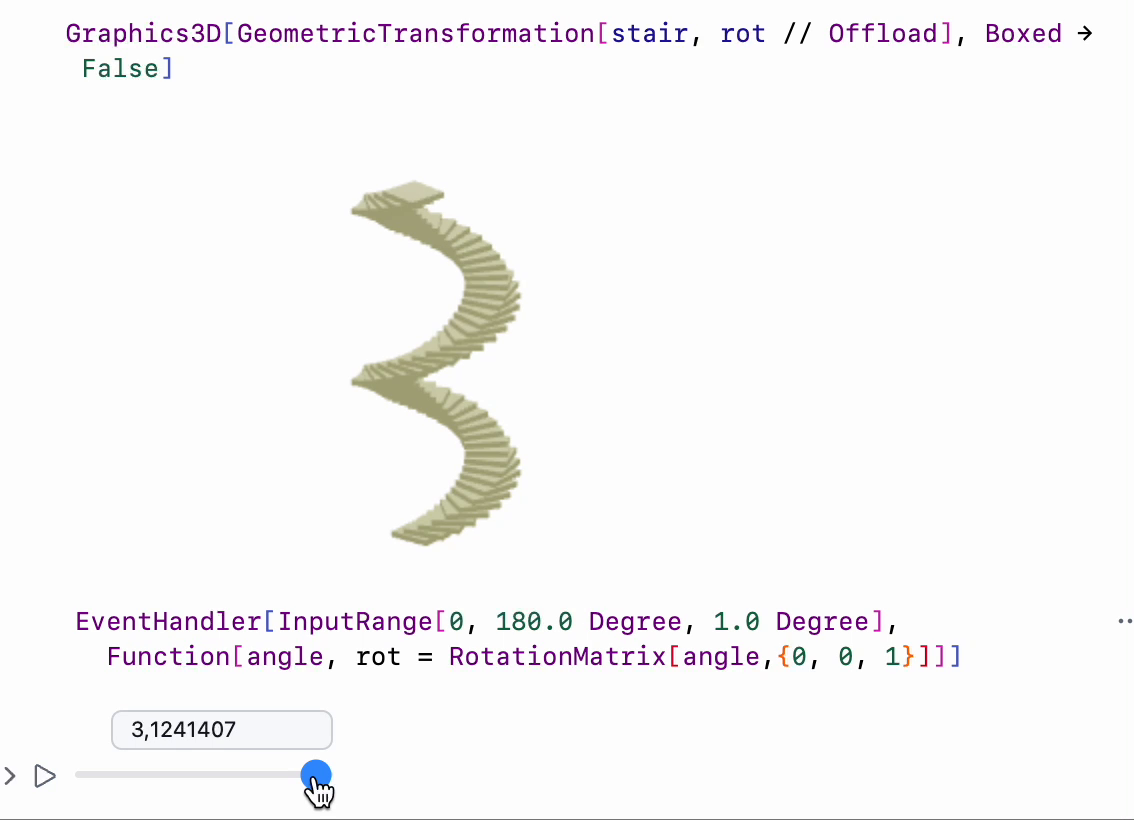
Graphics3D[GeometricTransformation[stair, rot // Offload], Boxed -> False]
cell 2
EventHandler[InputRange[0, 180.0 Degree, 1.0 Degree],
Function[angle, rot = RotationMatrix[angle,{0, 0, 1}]]]
The result is following